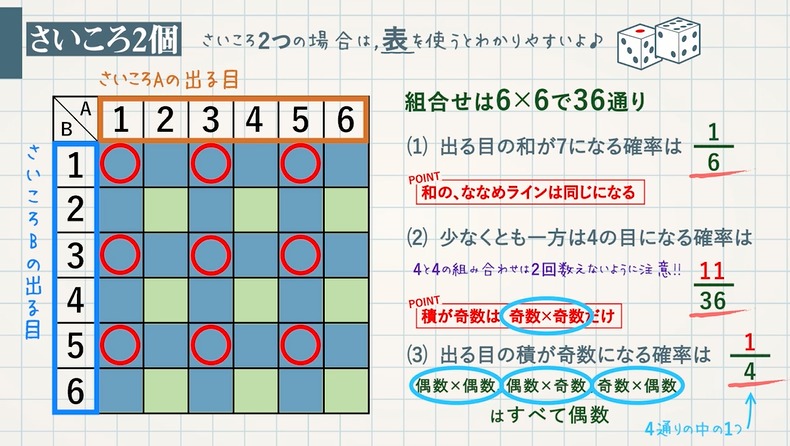
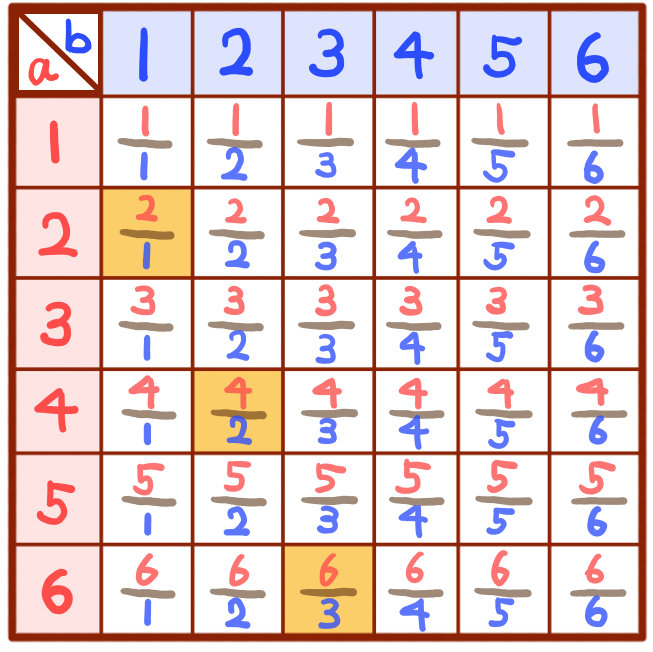
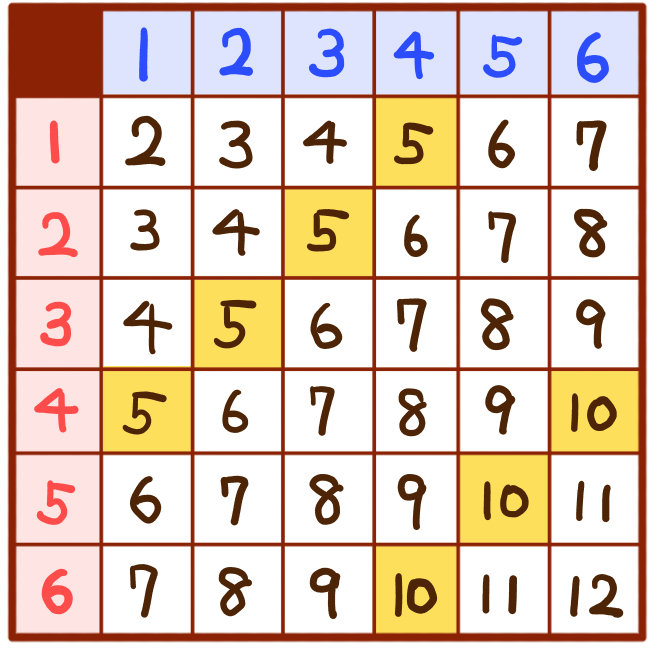
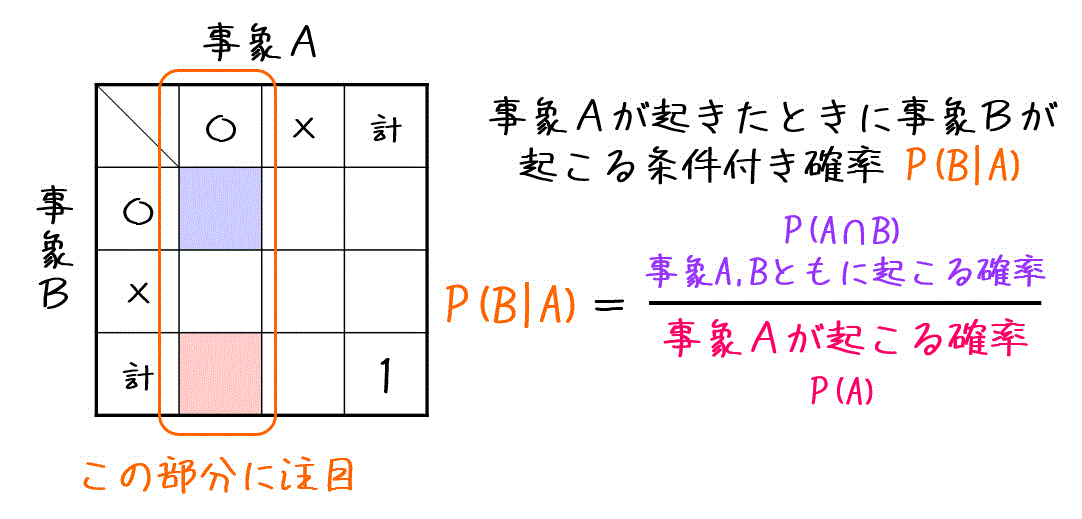
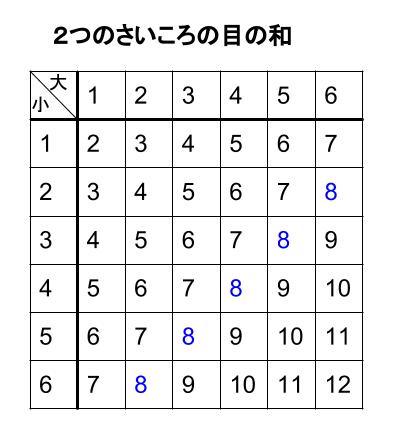
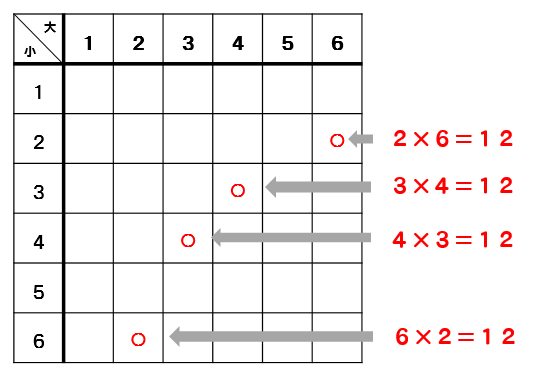
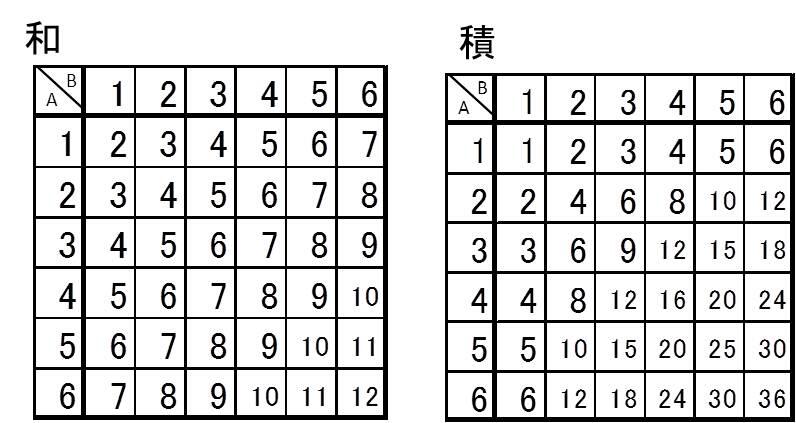
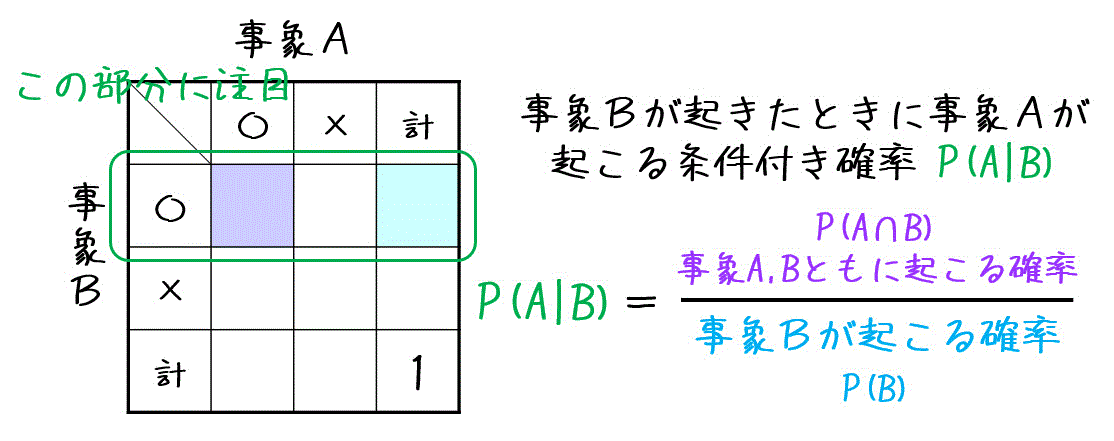
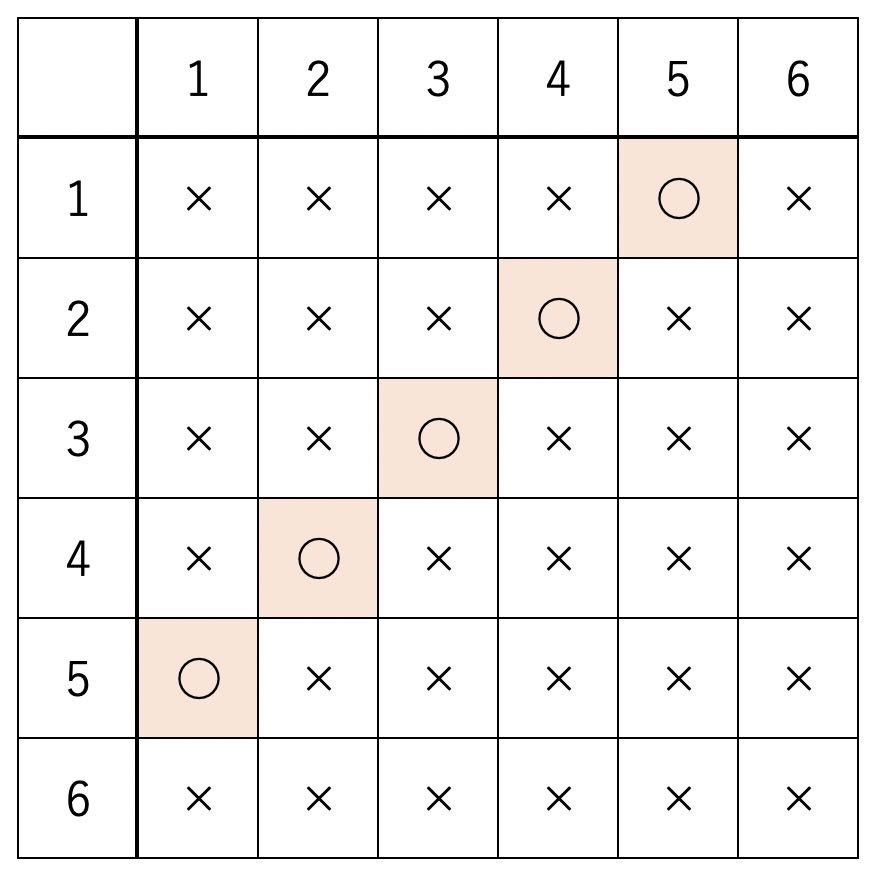
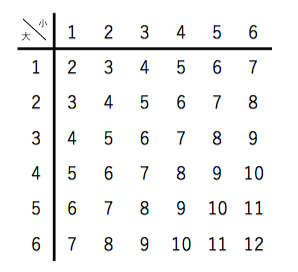
条件付き確率の定義は以下の通りでした。 ということは、今回の問題ではこのように数式を書くことができますよね。 p(奇数)=1/2であり、p(3以下かつ奇数)=2/6=1/3です。 よって、p(3以下奇
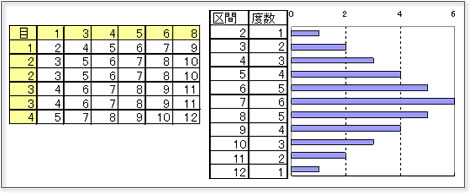
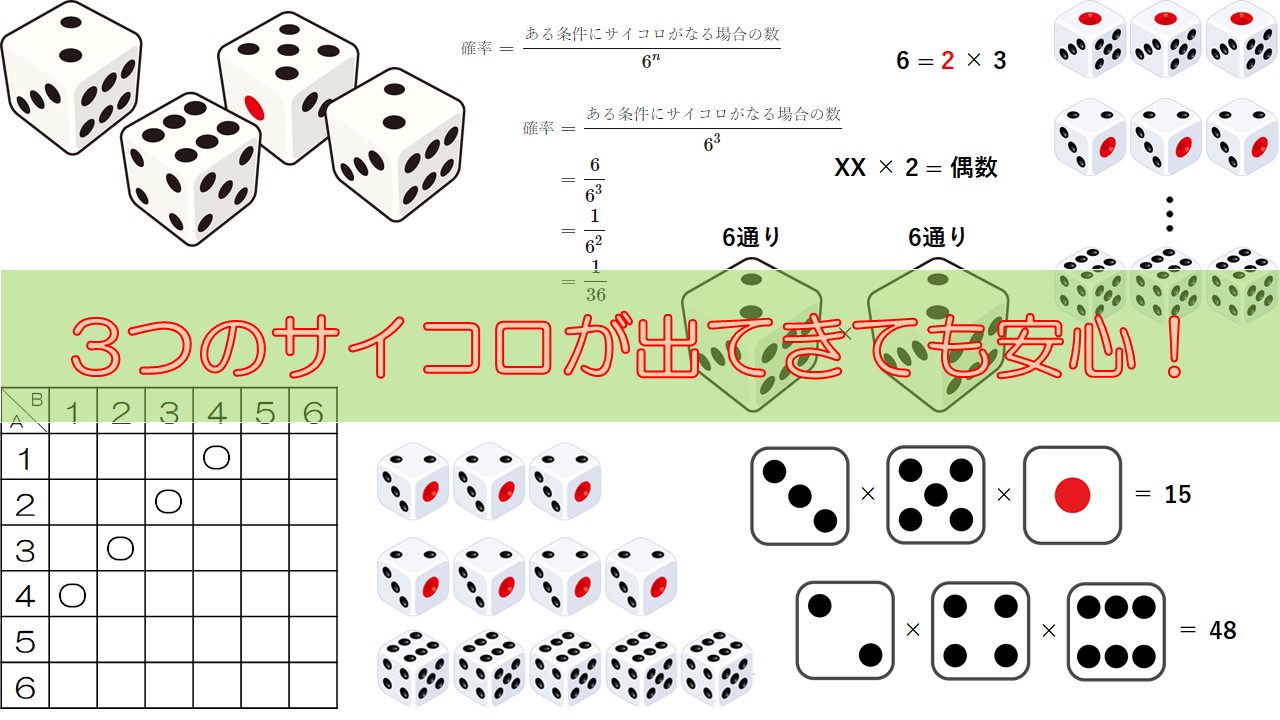
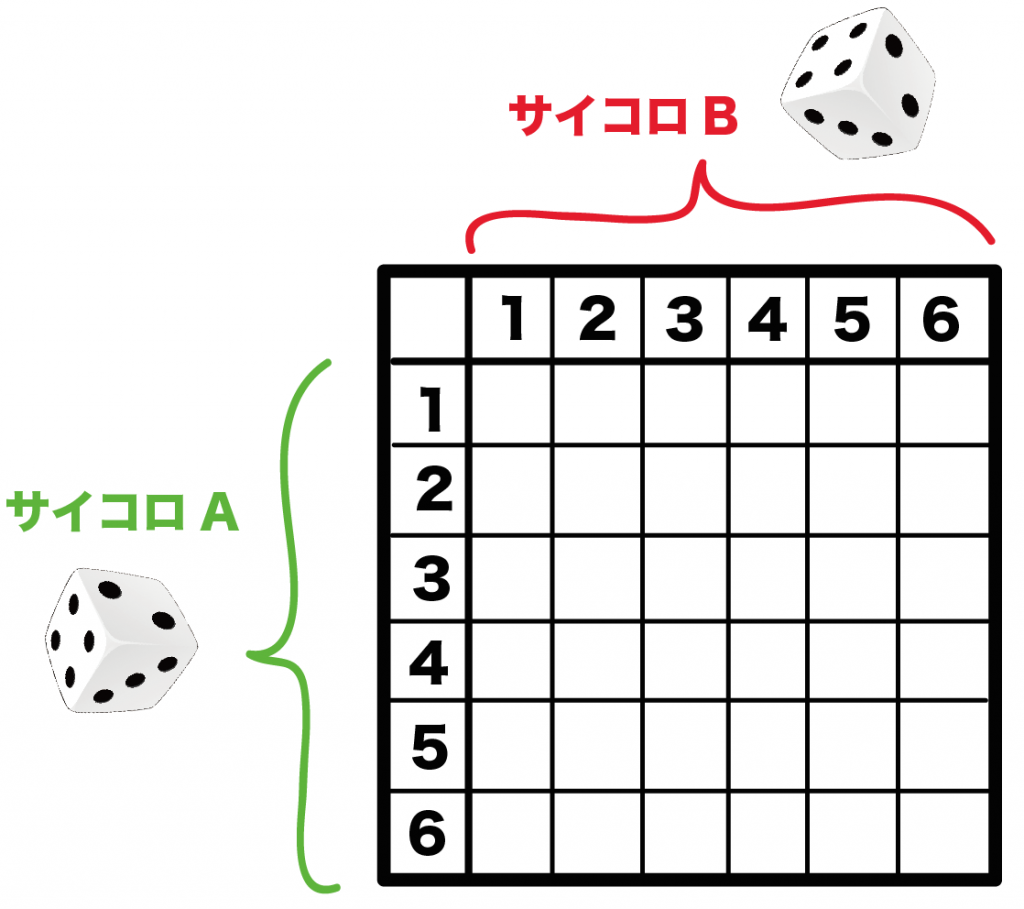
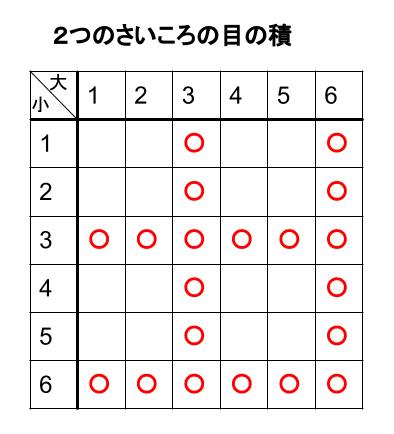
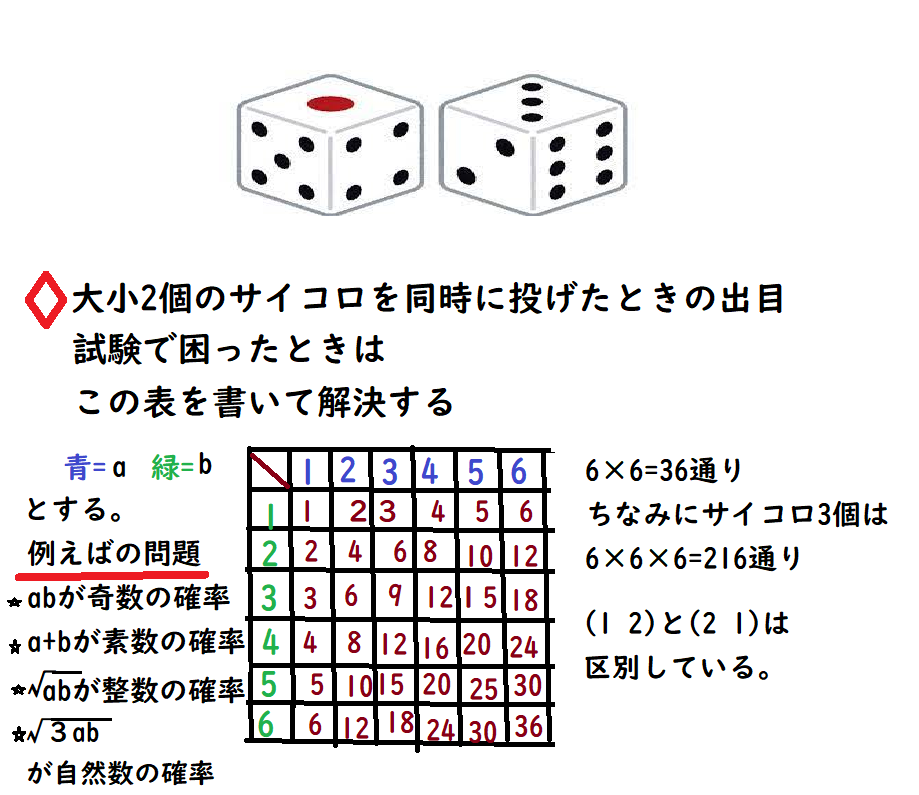
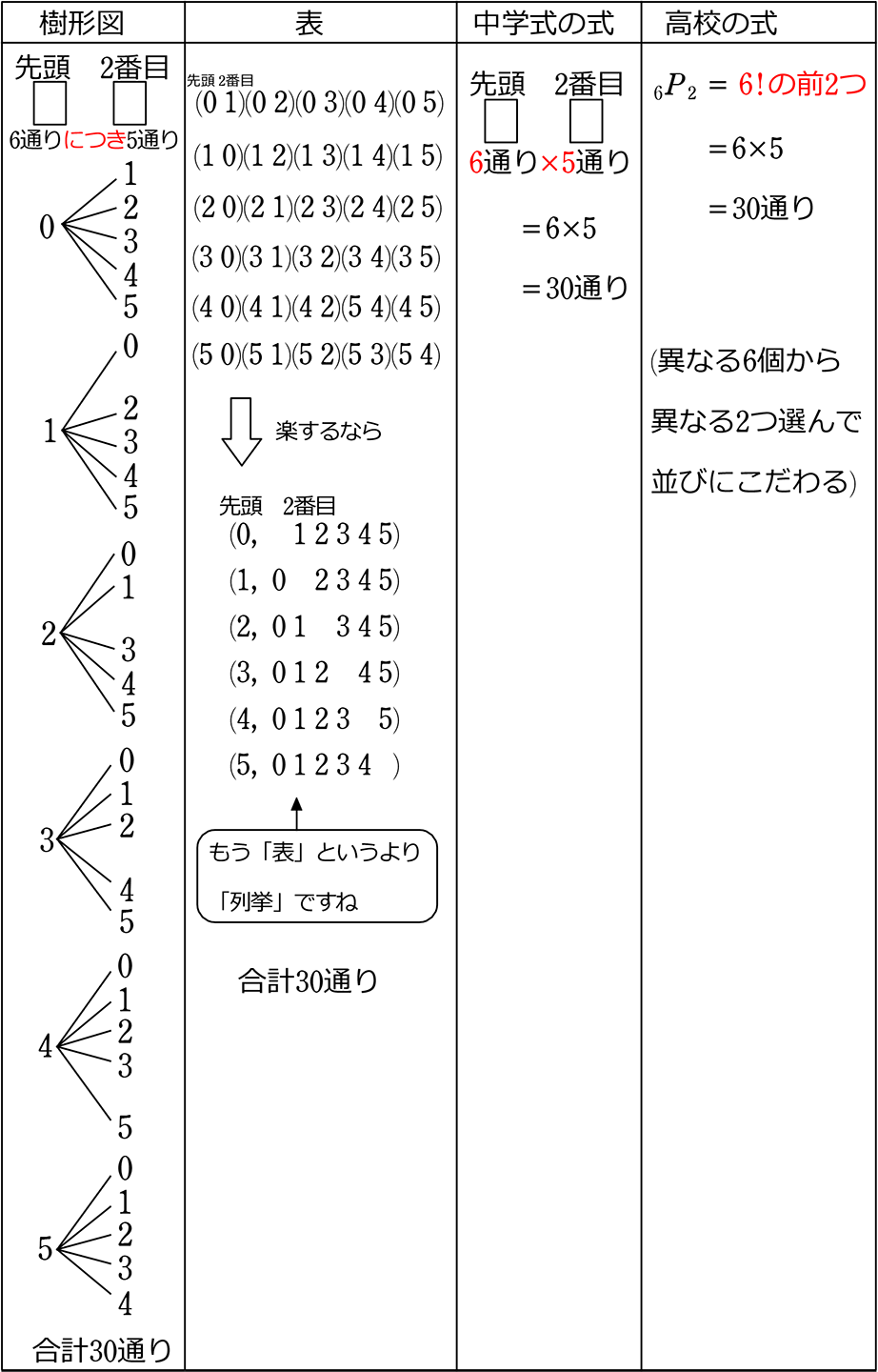
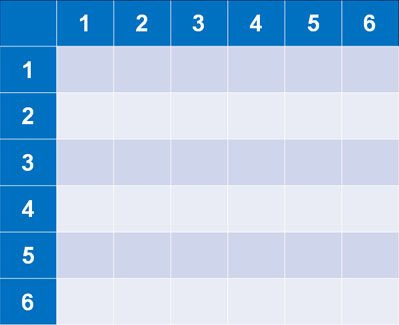
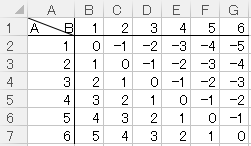
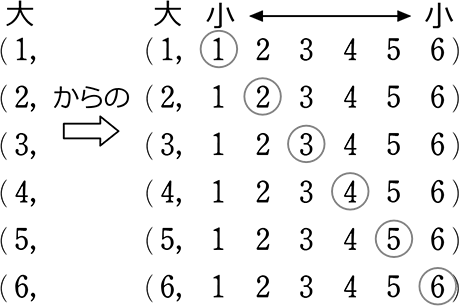
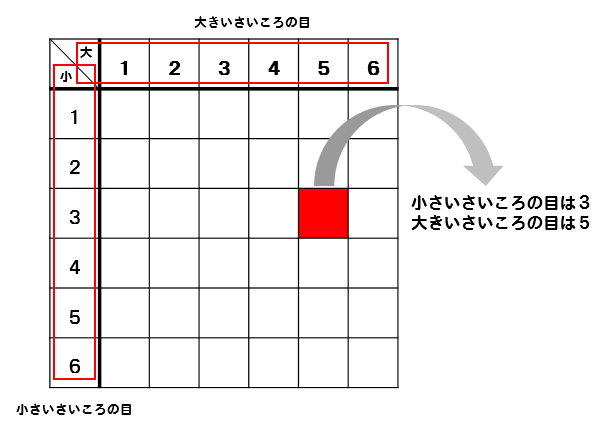
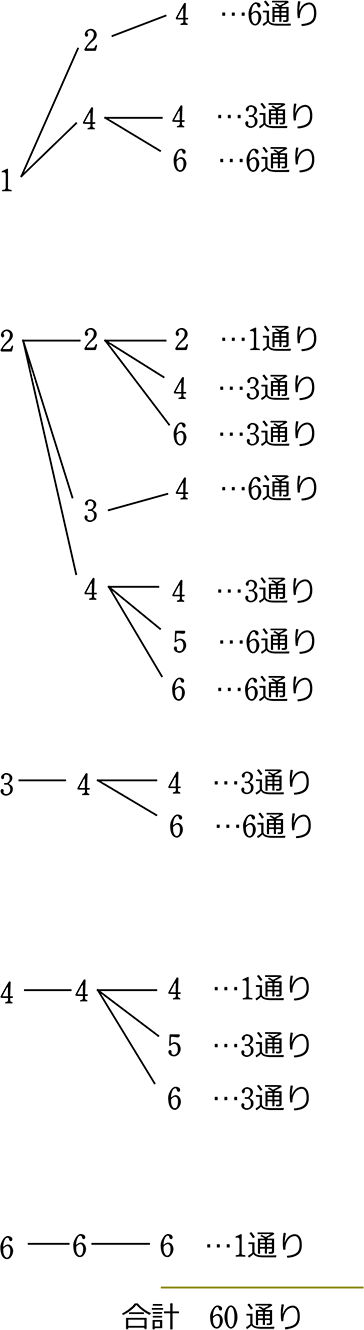
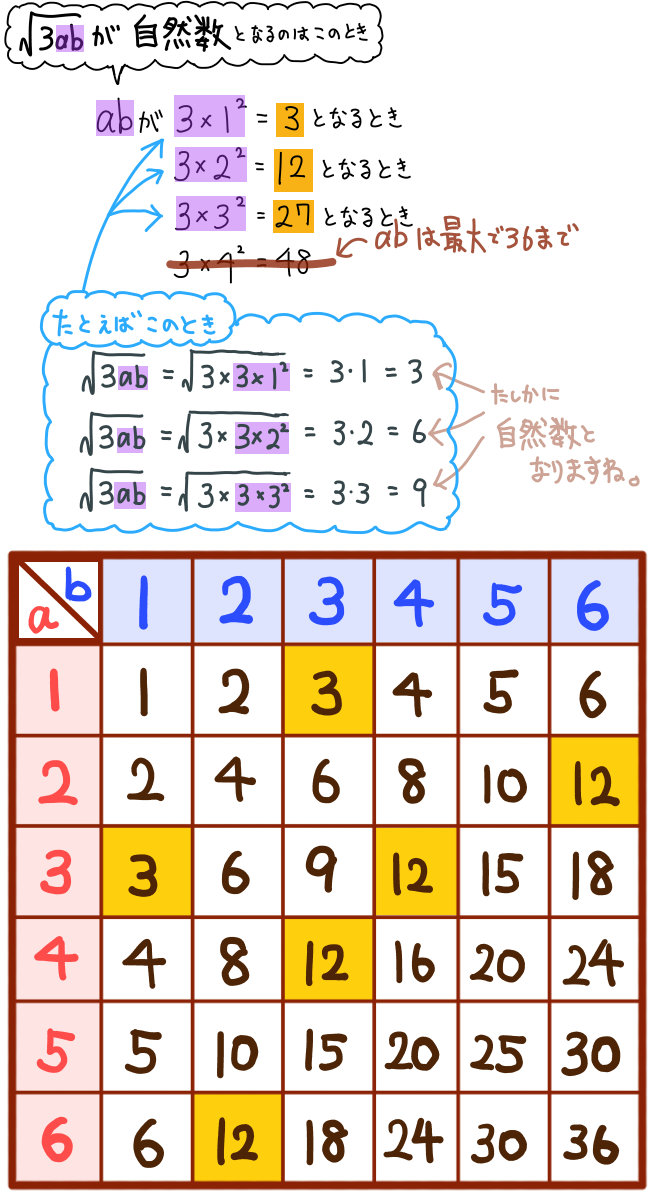
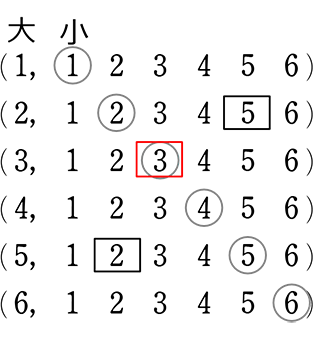
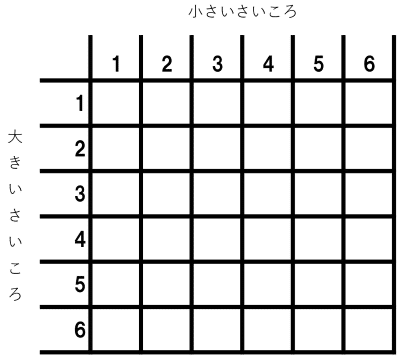
サイコロ 3つ 確率 表- 確率の問題であれば、表にすべて書くのは216通りあって大変なので、条件に適する組み合わせのみを書き出す手法をおすすめします。 例えば、 (条件) 3つのサイコロの出た目の和が17 サイコロの確率を教えてくださーい! かず先生 サイコロといっても 1つの場合、2つの場合 いろんなパターンがあるから、それぞれのパターンについて見ていこうか! というわけ
サイコロ 3つ 確率 表のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  | |
 |  |  |
 |  | |
「サイコロ 3つ 確率 表」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  | |
 |  | |
「サイコロ 3つ 確率 表」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
 |  |  |
「サイコロ 3つ 確率 表」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | 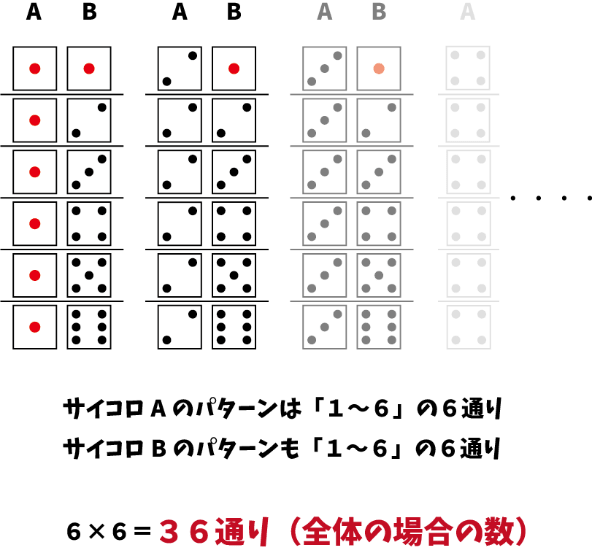 |
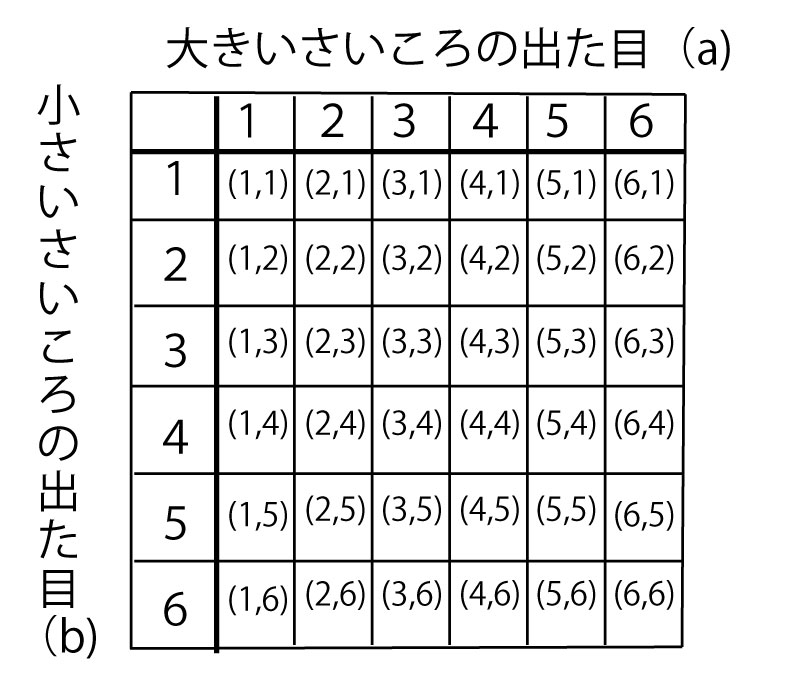 | 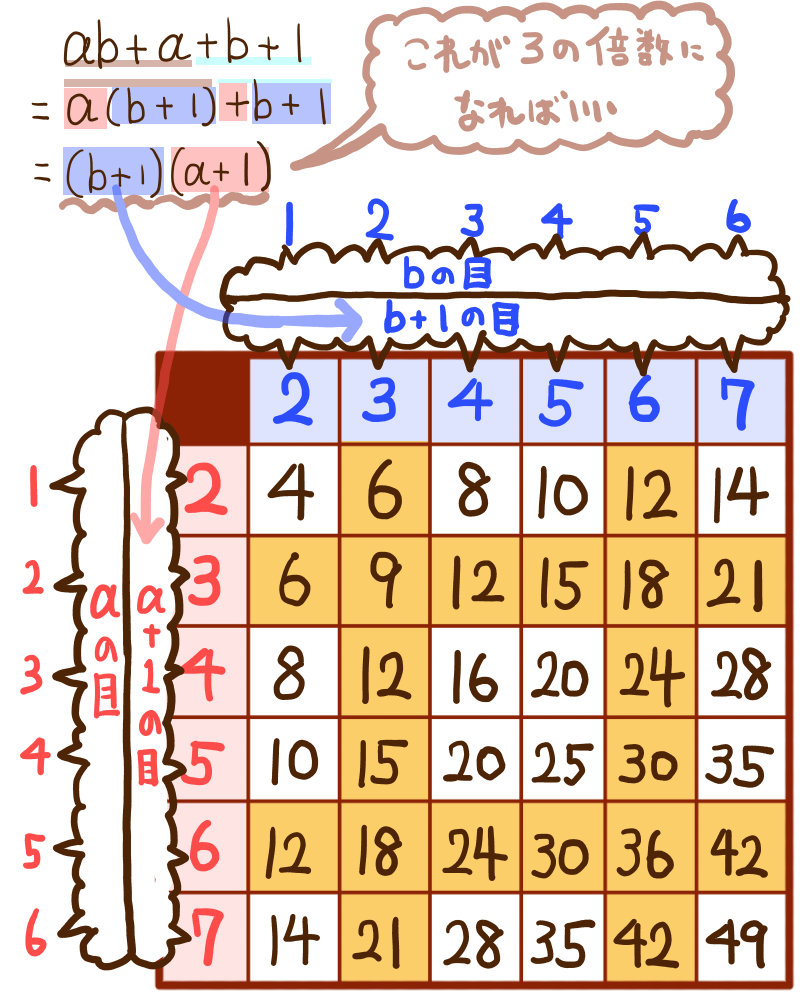 | |
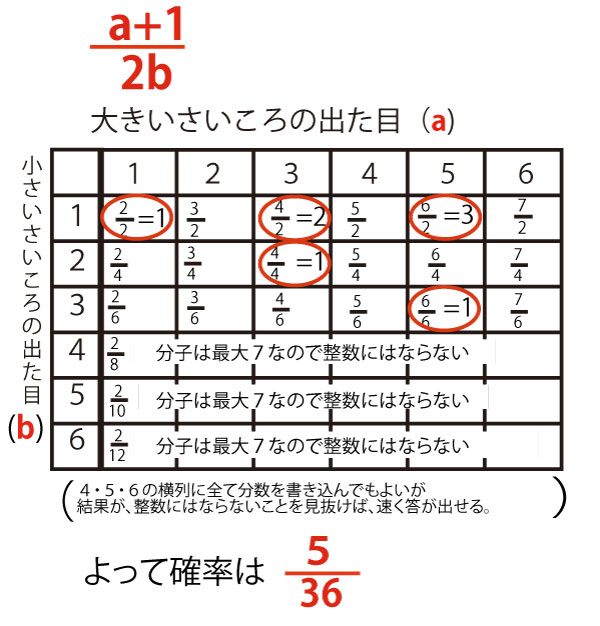 |  |  |
 |  | |
「サイコロ 3つ 確率 表」の画像ギャラリー、詳細は各画像をクリックしてください。
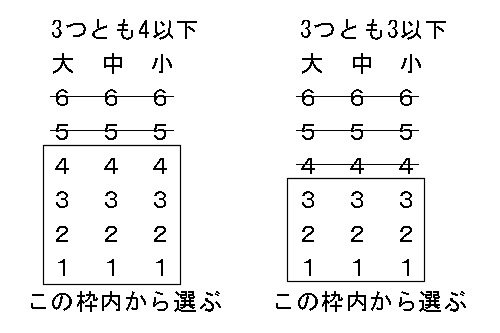 |  |  |
 |  |  |
 |  | |
 | ||
「サイコロ 3つ 確率 表」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「サイコロ 3つ 確率 表」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
 |  |  |
「サイコロ 3つ 確率 表」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
 |  | 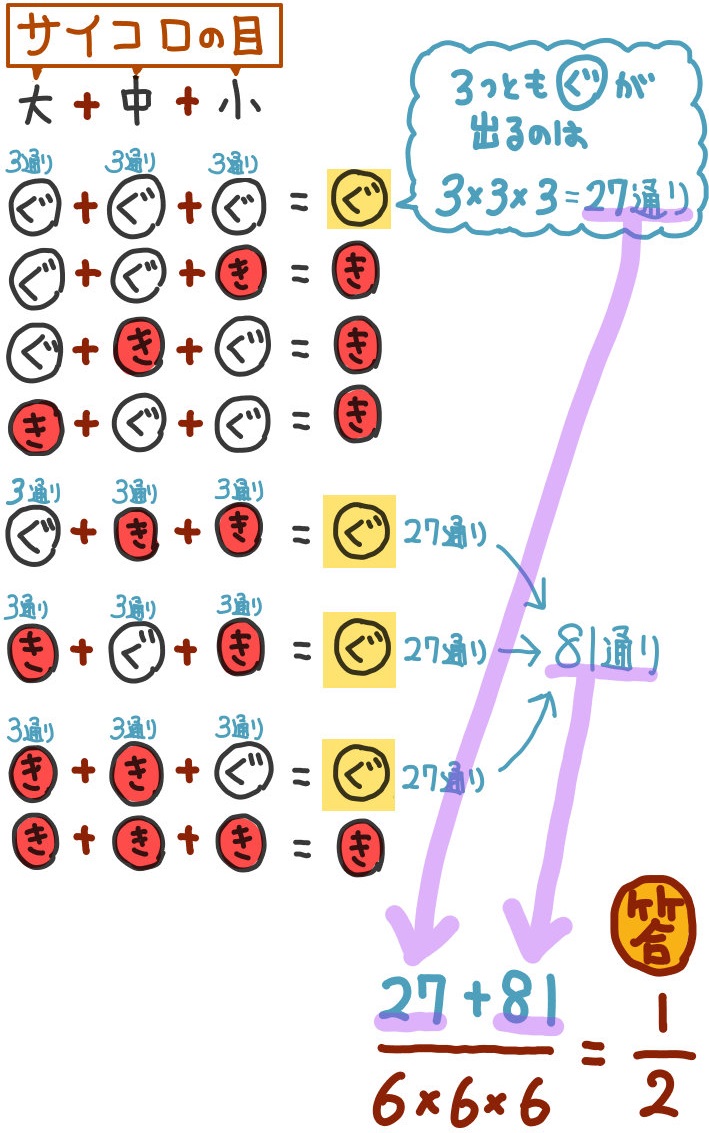 |
「サイコロ 3つ 確率 表」の画像ギャラリー、詳細は各画像をクリックしてください。
 | 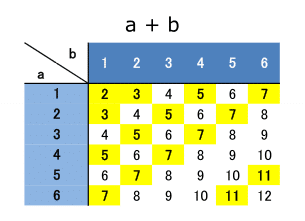 | 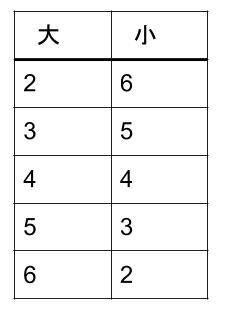 |
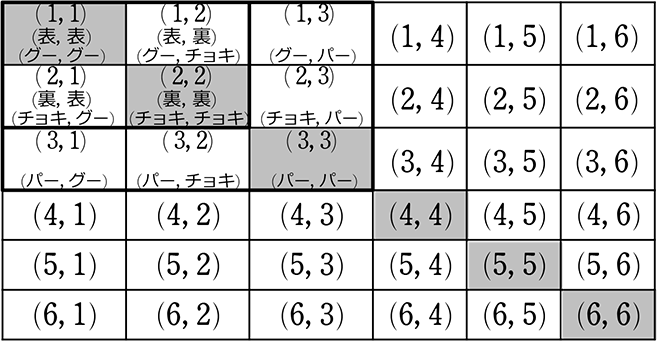 |  | |
 | 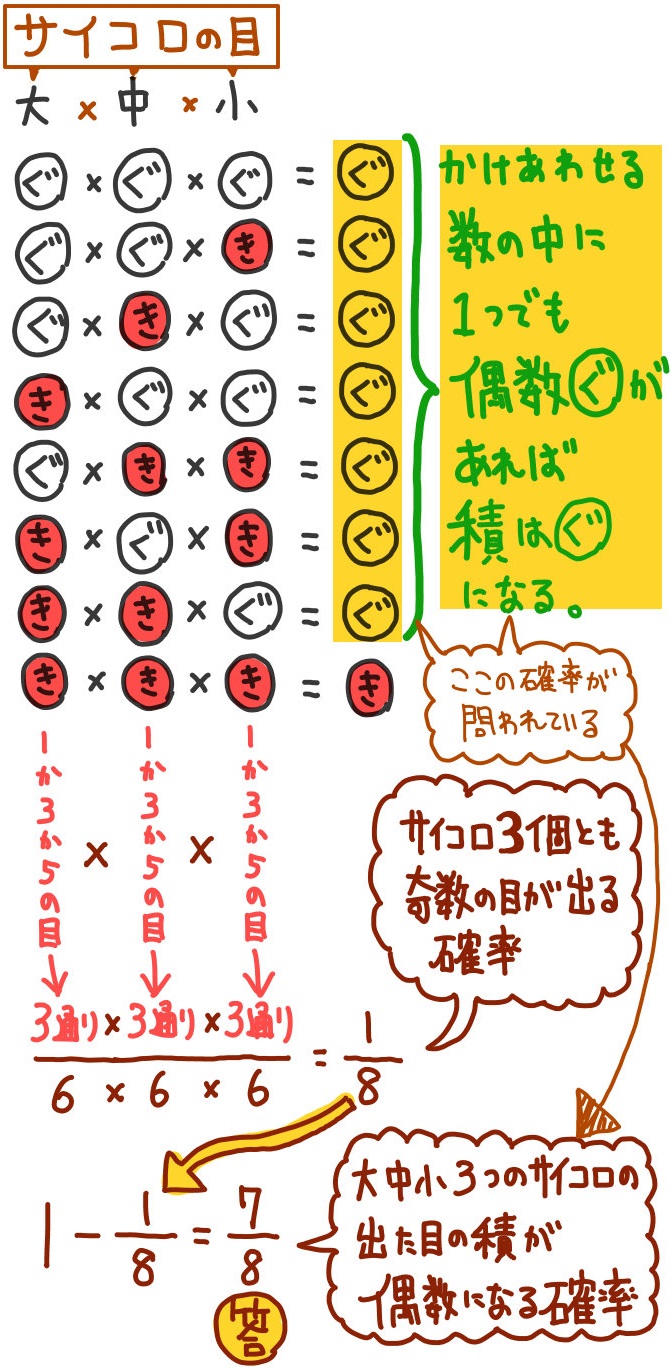 |
で出るインチキサイコロの出目の情報のエントロピーを求めてみましょう。エントロピーは、\ 3 \cdot \frac{1}{4} \log_2 \frac{1}{4} 3 \cdot 3標準偏差 4正規分布 5二項分布 6推測統計(t分布、カイ二乗分布) 7仮説検定 と、実務上必要な大体の範囲を押さえている。 たとえば、2項分布の例題として出題されている問題
Incoming Term: サイコロ 3つ 確率 表,




0 件のコメント:
コメントを投稿